SIR Model

The SIR Model is the most famous epidemiologic model. It considers the population that belongs to each of the following states:

1. Susceptible (S) - the individual has not contracted the disease, but the individual can be infected due to transmission from infected people.
2. Infected (I) - This person has contracted the disease.
3. Recovered/Deceased (R) - This person either survived, hence recovered, or has died, hence deceased.

β is the parameter for transmission rate, and γ is the recovery rate. On the right, you have ordinary differential equations that summarize this model in a short-term deterministic model. This ignores vital dynamics (ie. new births, for a growing population) so it is a closed population.

The graph should make sense. Overtime, the number Susceptible (S) decreases, the number Recovered/Deceased (R) increases, and the number Infected (I) increases to a peak then drops back down.

I solve the differential equations using a 4th order Runge-Kutta method.

I decided to change my model to the superior SEIR Model:

SEIR Model

This has an “Exposed” compartment which is ideal for infections that have a significant incubation period during which individuals have been infected but are not yet infectious themselves.

α is the parameter for the average incubation, and μ is the death rate.

This is an excellent SEIR-model calculator for COVID

So to re-iterate:

1. S ==> Susceptible : number of susceptible
2. E ==> Expose : number of exposed
3. I ==> Infectious : number of infectious
4. R ==> Recovered or Removed : number recovered (or immune) individuals.
   • We have S + E + I + R = N, this is only constant because of the (degenerate) assumption that birth and death rates are equal, N is country population.

There’s also a few other variables:

• R_0 & R_t ==> Reproduction number: The definition describes the state where no other individuals are infected or immunized (naturally or through vaccination)
• T_inf ==> Average duration of the infection, 1/T_inf can be treat as individual experiences one recovery in D units of time.
• T_inc ==> Average incubation period, Many paper and article define as 5.1 (reference, reference2)

The R_0 can decrease from intervention measures such as government isolation/lock-down, vaccinations, etc.

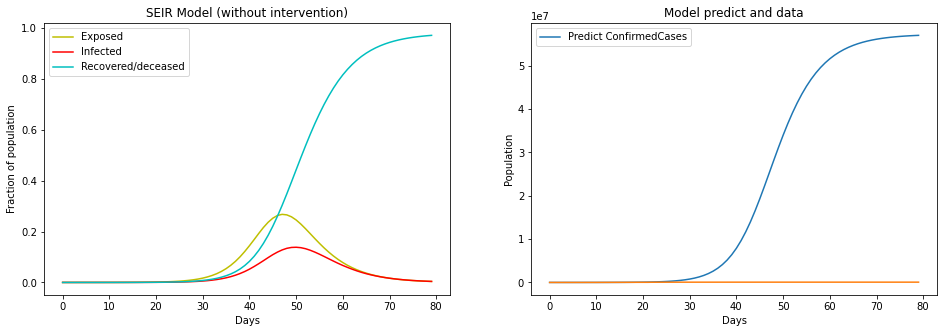
Here’s an example of the SEIR model on Hubei without intervention:

Now, with intervention:

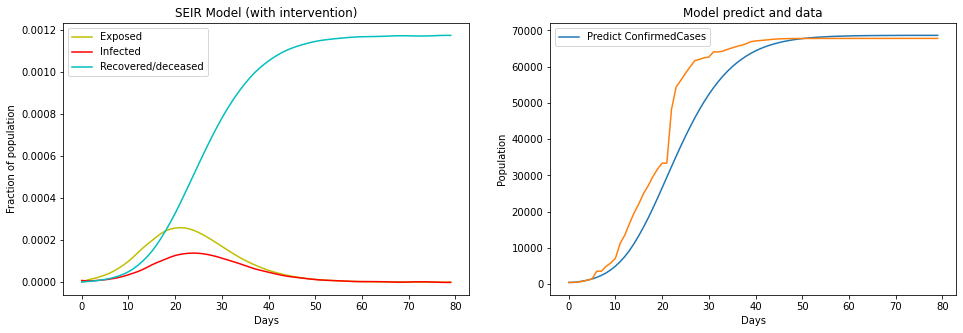
A substantial difference as you can see.

In models with intervention, we can reduct R_t by using differential decay functions, like the Hill Function.

The Hill Function represents a half-decay that never reaches zero due to its exponential nature.

I find that the average incubation period (T_inc) is 5.2, and the average infectious period (T_inf) is 2.9.

As for R_t, I find this number by fitting the real data to the SEIR model’s curve. Same goes for cfr, or Case Fatality Rate.

Given that the Hill Function involves the R_0 to half each time, that is what I set as the function for the total period of time that intervention is enforced. I think 80 days is a good average.

So, once intervention begins, R0 = R0 * 0.5.

TL;DW (too long, didn’t write especially considering the hour) so I’m just going to link my code here it’s relatively self-explanatory.

Let’s just throw some relevant forecasting curves up first:

United States

New York

Global

My SEIR Model Code

My SEIR Model Code